Az algebra újrafelfedezése: így oldják meg a lehetetlent
A polinomiális egyenletek megoldása évszázadok óta meghatározó része a tudománynak; elég csak a csillagászat, a számítógépes grafika vagy a piaci növekedési előrejelzések területére gondolni. Míg az egyszerűbb polinomegyenleteket minden középiskolás átlátja, a magasabb fokú polinomegyenletekkel már a professzionális matematikusok is nehezen boldogulnak. Most azonban a New South Wales-i Egyetem (University of New South Wales) egyik matematikusa és egy független informatikus, Dean Rubine, kidolgozta az első általános módszert ezeknek az „ördögi” egyenleteknek a megoldására.
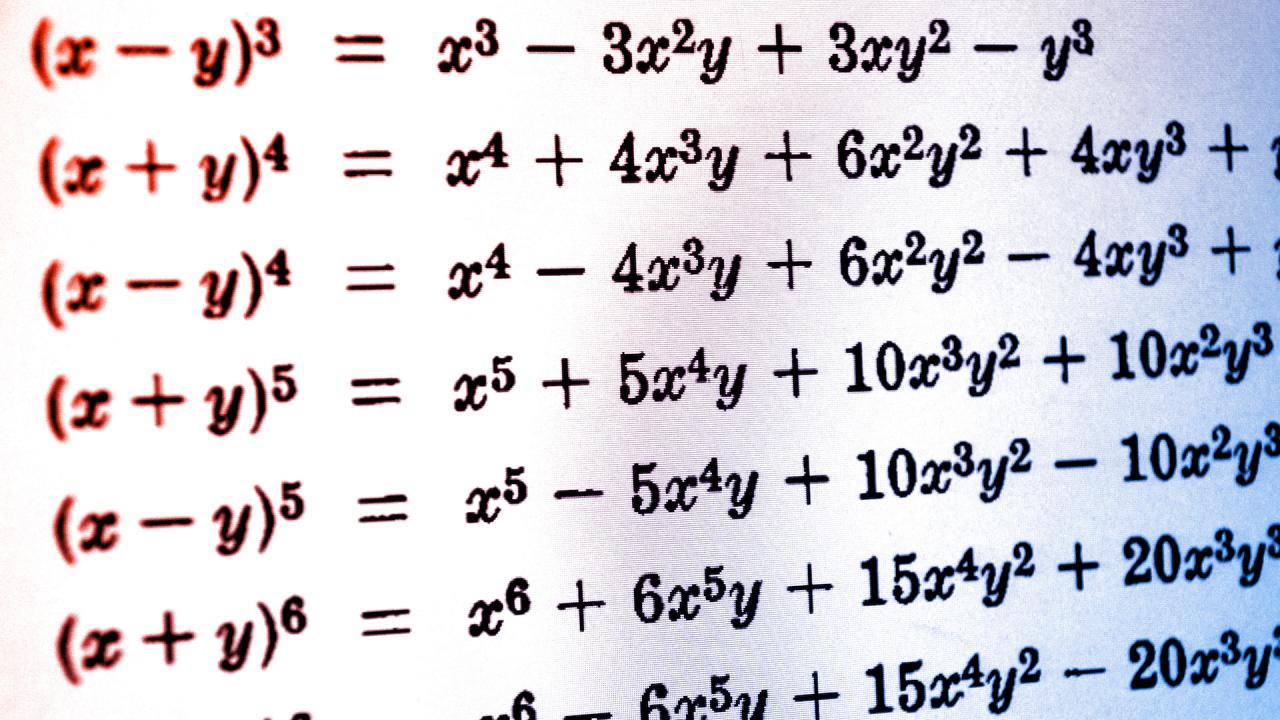
Radikálisok helyett határtalan sorozatok
A polinomok olyan algebrai egyenletek, amelyekben a változókat nem negatív egész kitevőre emeljük – például x² + 5x + 6 = 0. Az első- és másodfokú egyenletek bizonyítottan megoldhatók a jól ismert gyökös képletekkel, de ezek általában irracionális számokat eredményeznek, amelyek végtelen tizedesjegyűek, ezért teljesen pontos, általános megoldás nincs rájuk. A problémát tovább nehezíti, hogy már az ötödik fok felett sosem sikerült univerzális formulát találni, mivel az irracionális számokhoz elméletileg végtelen számítási kapacitásra lenne szükség – mondta Norman Wildberger matematikus.
Az áttörést a „Geode” hozta meg
Az új módszer a magasabb fokú polinomokat a radikálisok és az irracionális számok használata nélkül oldja meg: helyettük úgynevezett hatványsorokat alkalmaz, amelyek végtelen számú x-hatványból állnak. Ezek a matematikán belül a kombinatorikához kapcsolódnak. A módszer a Katalán-számokra épül, amelyek azt írják le, hányféleképpen lehet egy sokszöget háromszögekre bontani. A Katalán-sorozatot először Mingantu mongol matematikus írta le 1730 körül, majd Euler is felfedezte 1751-ben. Wildberger és Rubine rájöttek, hogy a Katalán-számok általánosításával, a „Geode”-dal általános eszközt adhatnak a magasabb fokú polinomok megoldásához. Ennek az áttörésnek a jövőben különösen nagy jelentősége lehet a számítástechnikában és a grafikai modellezésben.
“Wallet biopsy” Szó szerint: pénztárca-biopszia 💸, amikor egy orvos vagy egészségügyi szolgáltató előbb ellenőrzi 🔬, mennyi pénzed / biztosításod van, és aztán dönti el, milyen vizsgálatot kapsz...
Sir Roger Penrose brit matematikus és elméleti fizikus, aki a fekete lyukak szingularitásának és az általános relativitáselmélet új matematikai alapjainak feltárásáért kapott Nobel-díjat, az 1970-es években sokkoló, a tudományos világot megosztó tézist közölt...
Az élelmiszerpazarlás világszinten óriási problémának számít: évente több mint 1 milliárd tonna étel végzi hulladékként, ennek mintegy 60 százaléka a háztartásokból származik...
Jól szemlélteti ezt, hogy a tudósok egy 3,4 millió éves, úgynevezett „Burtele-láb” maradványai alapján új fejezetet nyitottak az emberi evolúció történetében Etiópiában...
💡 Világszerte mintegy 40 millió ember él HIV-fertőzéssel. Bár az orvostudomány fejlődése révén a betegség ma már nem jelent automatikus halálos ítéletet, a teljes gyógyulás eddig elérhetetlen maradt...
🛰 Fontos kérdés, hogy több mint hetven évvel ezelőtt Kaliforniában, a Palomar Obszervatórium csillagászai különös, csillagszerű fényvillanásokat fotóztak az égbolton: ezek a pontok egy órán belül megjelentek, majd eltűntek — mindez jóval az első műhold, a Szputnyik–1 (Sputnik 1) fellövése előtt...
A papíron egyszerű számolással ki lehet számolni, hogy a nyugdíj optimalizálásának legjobb módja, ha valaki minél később, akár 70 évesen igényli a társadalombiztosítási ellátást...
🏃 A rendszeres mozgás rengeteg egészségügyi előnnyel jár: csökkenti a szívbetegségek, a rák és a korai halálozás esélyét, javítja a testi-lelki állapotot...
Az Európai Bizottság vizsgálatot indít, hogy az Apple hirdetési szolgáltatása, az Apple Ads, és térképszolgáltatása, az Apple Maps a Digital Markets Act (DMA) nevű szabályozás szigorú előírásai alá tartoznak-e...
