A mesterséges intelligencia végre magától tanul

Az MI fejlesztésében régóta nagy kihívás, hogy a gépek hatékonyan sajátítsák el a világ működését az emberek beavatkozása nélkül. A Joint-Embedding Predictive Architectures (JEPA) módszertana ígéretes ugyan, de eddig kevés elméleti alapot és gyakorlati útmutatást kapott; a kutatás ezért inkább ad hoc megoldásokra támaszkodott. Erre kínál megoldást a LeJEPA, egy letisztult, skálázható, elméletileg megalapozott tanulási célfüggvény.

Izotróp Gauss-eloszlás: a kulcs az önálló tanuláshoz

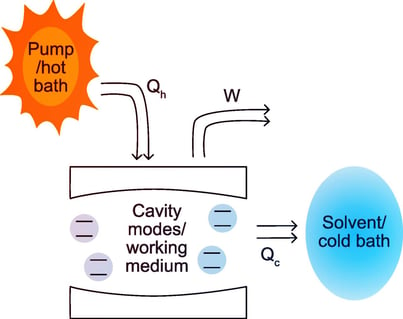
A kutatók kimutatták, hogy az úgynevezett izotróp Gauss-eloszlás a legalkalmasabb, ha azt szeretnénk, hogy az MI pontos előrejelzéseket adjon. Ezt az új célt a Sketched Isotropic Gaussian Regularization (SIGReg) nevű módszerrel sikerült kikényszeríteni, amely átstrukturálja az MI által generált reprezentációkat, hogy azok valóban megfeleljenek az optimális eloszlásnak.

Stabilitás, egyszerű kezelés, gyors implementáció

A LeJEPA módszer stabilan működik bármilyen hálózati architektúrán (ResNet, ViT, ConvNet), nincs szükség trükkökre, mint a stop-gradient vagy a teacher–student, és nem igényel bonyolult hiperparaméter-kezelést sem. Egyetlen kompromisszumos paraméter is elegendő, ráadásul az egész bevezetése mindössze 50 sornyi kóddal megoldható. Kiterjedt teszteken bizonyított: több mint 10 adatbázison és 60 különböző MI-architektúrán, változatos feladatokon működött. Az ImageNet-1k adatbázison például 79 százalékos pontosságot ért el ViT-H/14 hálózattal, befagyasztott alaphálóval.

Vissza az alapokhoz az MI-ben

A LeJEPA egyszerűsége és szilárd elméleti kerete új életet lehelhet az önfelügyelt előtanulásba – visszahozva ezt a megközelítést az MI-kutatás középpontjába.

2025, adrienne, arxiv.org alapján