Solitonok és az integrálhatóság jelentősége
A szoliton rövid, de stabil hullámcsomag, amely elméletileg végtelen ideig megőrizheti az alakját, még más hullámokkal való kölcsönhatás után is. Ehhez úgynevezett integrálhatóság szükséges, vagyis a rendszerben az olyan megmaradó mennyiségek, mint az energia és a lendület, mindvégig változatlanok maradnak. Ez teszi a szolitont ellenállóvá a torzulással és a turbulenciával szemben, amelyek más különleges hullámtípusokat könnyen tönkretehetnek.
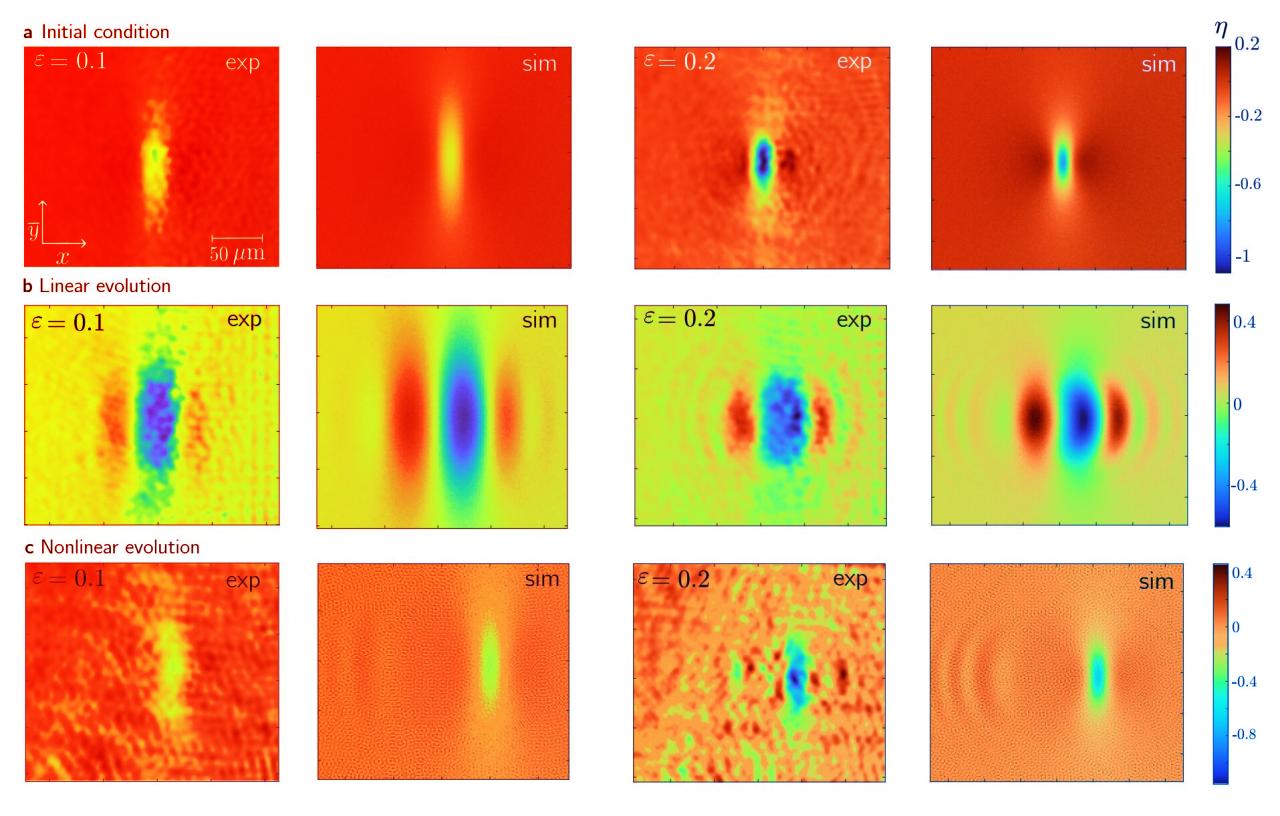
Korábban már sikerült laborban szolitonokat létrehozni, ezek azonban mindig csak egy dimenzióban, azaz egyenes vonalban terjedtek. 1970-ben szovjet fizikusok azonban megalkottak egy modellt, amely szerint létezhetnek háromdimenziós szolitonok is: ez a „lump-szoliton”, amelyet a Kadomtsev–Petviashvili-egyenlet (KP egyenlet) ír le. Azóta a kutatók igyekeztek kísérletileg igazolni, de a szigorú matematikai feltételek miatt ez mostanáig csak elméleti lehetőség maradt.
Kísérleti áttörés és jövőbeli lehetőségek
A Sapienza kutatói stroncium–bárium–niobát kristályt használtak, amelynél a fény intenzitásfüggő viselkedése feszültséggel szabályozható. Így egy kétdimenziós „fotonfolyadékot” hoztak létre, amely a feszültség hatására úgy folyik, mint egy klasszikus folyadék. Ez lehetővé tette, hogy mikrométeres pontossággal beállítsák a fény amplitúdóját és fázisát is – ez elengedhetetlen a szoliton kezdeti állapotának pontos előállításához.
Ezzel a módszerrel sikerült olyan többdimenziós, valóban integrálható szolitont létrehozniuk, amely mindezidáig lehetetlennek tűnt. A laborban előállított lump-szoliton megőrizte formáját, sőt, amikor egy másik, szemből érkező szolitonnal ütközött, akkor is stabil maradt. Ez a hullámforma ellenállóságának egyértelmű bizonyítéka.
A csapat bízik abban, hogy eredményeik új lehetőségeket nyitnak a háromdimenziós szolitonok vizsgálatában és a nemlineáris hullámok kutatásában, mivel minden eddiginél nagyobb pontossággal sikerült reprodukálniuk az elméleti hullámalakokat.