Kiemelt szerepben a mozgás paraméterei
Lényeges szempont, hogyan módosítják a kinematikai paraméterek változásai a kozmológiai összefüggéseket. Az ilyen változásokat általában differenciálegyenletekkel írják le, amelyek számos fizikai folyamat dinamikáját modellezik. Ezek az egyenletek alkotják a kozmológia gyakran igen bonyolult matematikai hátterét, amely megmutatja, miként alakultak az összefüggések az univerzum különböző korszakaiban.
Egy nemzetközi kutatócsoport, melynek tagjai többek között a Princetoni Egyetemen, a Caltechen, a Pisai Normál Főiskolán és a Chicagói Egyetemen dolgoznak, most egy újszerű keretrendszert mutatott be. Módszerük, a „kinematikai áramlás”, forradalmi irányt jelöl ki a bonyolult egyenletek kezelésére: alapvető kombinatorikai szabályok alapján vezetik le az általános képleteket, elhagyva a felesleges időbeli fejlődést.
Ábrák, csövek és szabályok
A kutatás egyik fontos újdonsága, hogy az aktuális matematikai egyenletek leírását képekkel, ábrákkal helyettesítik, és ezek alakzatai alapján jósolják meg, milyen összefüggések fognak előbukkanni. Pimentel, a kutatás vezetője elmondta, hogyan vált világossá előttük egy különleges mintázat: ha az ábrákat – amelyeket szeletekre bontottak, csöveket rajzoltak, majd különféle színkódos szabályokat alkalmaztak – egy sajátos szabályrendszer szerint manipulálták, minden formulasor előállíthatóvá vált.
A módszerben először megvizsgálják az adott korrelátor kinematikai terét: ez a két mennyiség kapcsolatának „térképe”. Ezt a teret aztán különféle lépésekben feldarabolják, a darabokat „csövekké” alakítják, majd hol összeolvasztják, hol elnyelik egymást – mindez pontos szabályok szerint, amelyek végül visszavezethetők az eredeti matematikai egyenletekre.
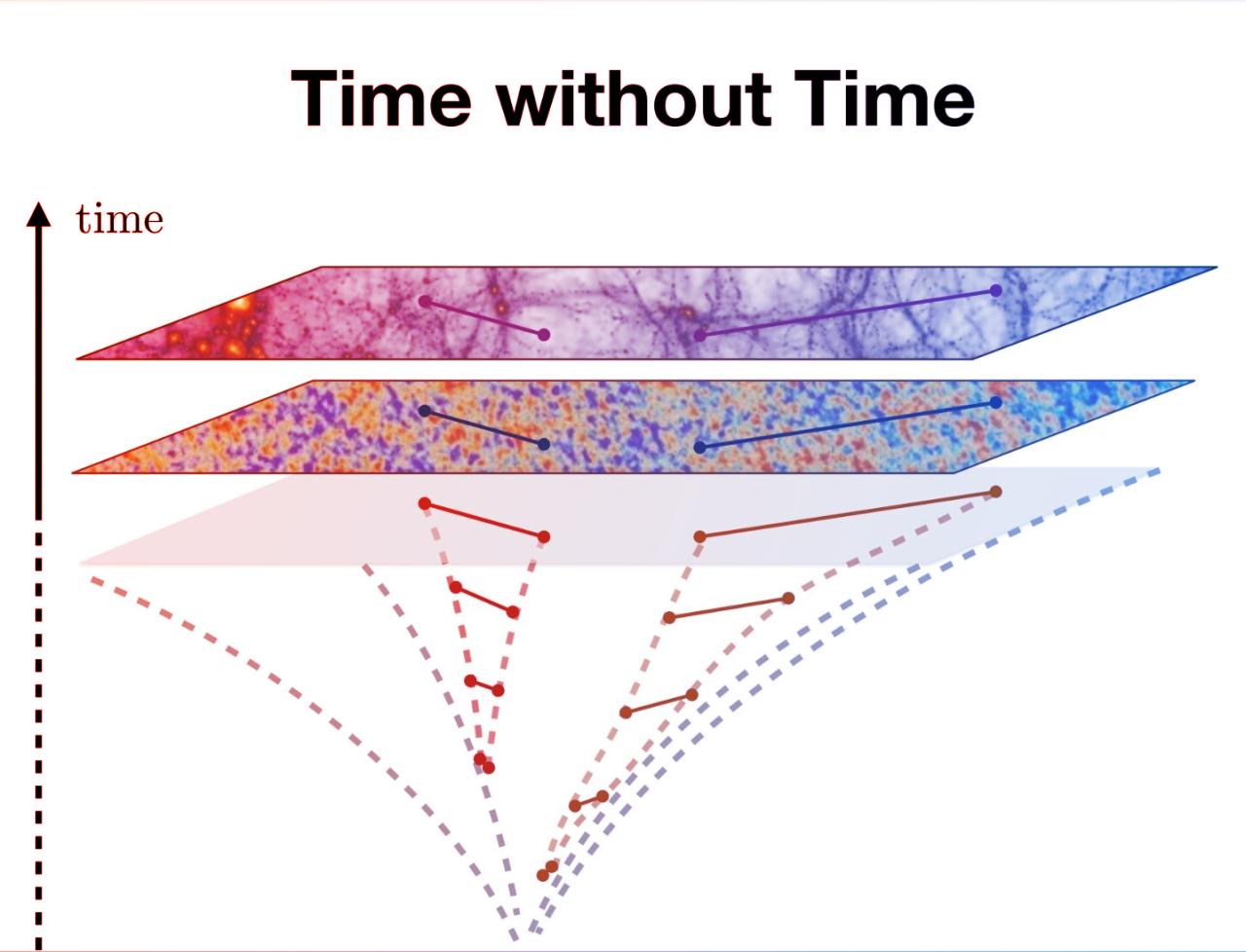
Idő nélküli univerzum?
Ennek ellenére az új megközelítésben nincs szükség arra, hogy előrehaladó idővel magyarázzunk bármilyen változást. Emiatt a térbeli elkülönülések, vagyis a „ki hol helyezkedik el?” kérdései önmagukban is elegendőek lehetnek a múlt kozmológiájának feltérképezésére. Az új szemléletmód remekül illeszkedik a kvantumgravitáció egyéb irányzataihoz, például a határ-obszervábilisokhoz vagy a téridő emergenciájának fogalmához.
A kutatásban alkalmazott új eszközök és trükkök más területekről is származnak: a kombinatorika például elvileg bármilyen rendszer leírására használható, ahol az elemek különféle elrendezési lehetőségeit kell számításba venni. Emiatt a matematikusok és részecskefizikusok is egyre nagyobb érdeklődést mutatnak a megközelítés iránt.
Végtelen lehetőségek a jövő kutatásaihoz
Most úgy tűnik, a kinematikai áramlás fogalma új elméleti utakat nyithat meg a korai univerzum és a komplex fizikai rendszerek leírásában. A kutatók azt tervezik, hogy a jövőben realisztikusabb modellekhez is alkalmazzák a módszert, amelyek jobban hasonlítanak arra, ahogyan a világegyetem első pillanatai kinézhettek. Ugyanakkor új kihívást jelent a matematikában és a mesterséges intelligencia alkalmazásában az is, hogyan lehet a leírást fák helyett bonyolultabb, „hurkos” struktúrákra is kiterjeszteni. Pimentel már dolgozik egy új, forgó részecskéket is leíró elméleten; itt is feltűnnek olyan matematikai minták, amelyeket korábban csak részecskefizikai modellekben láttunk.
Ennek következtében a mostani eredmények nemcsak a múlt, hanem a jövő fizikai elméleteinek kialakításához is hozzájárulhatnak – sőt, akár azt is megkérdőjelezhetik, tényleg szüksége van-e a világegyetemnek az idő fogalmára, vagy elég, ha csak az elrendezéseket vizsgáljuk.