Kockák, testek, árnyékok: mi fér át min?
Azóta matematikusok újabb és újabb testek esetén vizsgálták ezt a tulajdonságot. Lényeges, hogy az ilyen problémákat általában konvex poliéderekre szűkítik, vagyis olyan testekre, amelyek lapjai sík felületűek, és nincs befelé horpadásuk. A leghíresebb platóni testek – például a dodekaéder vagy az ikozaéder – bonyolult szimmetriájuk miatt különösen nehezen elemezhetők ilyen szempontból. Sok minden elképzelhető, de sokáig csak a kockánál volt egyértelmű, hogy működik a Rupert-járat.
Az 1960-as években bebizonyosodott, hogy más szabályos testek, például az oktaéder és az ikozaéder esetén is létezhet olyan átjáró, amelyen egy második, ugyanolyan test átpréselhető. Ettől függetlenül úgy tűnt, minden konvex poliéderre igaz ez a tulajdonság – vagyis Rupert herceg szerencséje újra és újra igazolódott.
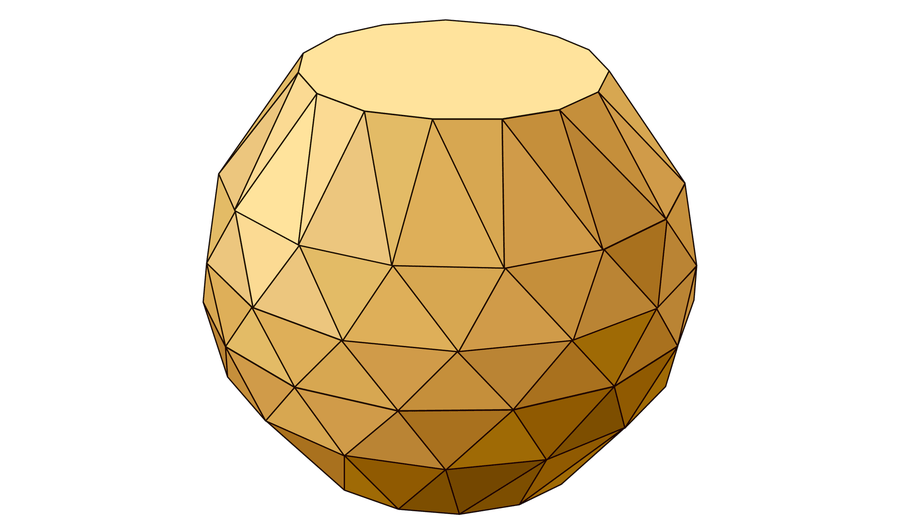
Megszületik a Noperthedron: az első ellenpélda
Minden eddigi próbálkozás ellenére a matematikusok csak sejtették, hogy létezhet olyan test, amelyen nem lehet Rupert-járatot fúrni. 2023 augusztusában azonban osztrák kutatók, Jakob Steininger és Sergey Yurkevich előálltak a Noperthedrónnal: egy egzotikus, 90 csúcsból és 152 lapból álló forma, amelyen – bizonyítottan – nem lehet átjuttatni önmagát egy egyenes alagúton.
A bizonyítás egyrészt elméleti áttörést, másrészt hatalmas számítógépes számításokat kívánt; a módszer a forma csúcspontjainak egészen speciális elrendezésén alapul. Maga Steininger is úgy fogalmazott: szinte csoda, hogy tökéletesen működik.
Az árnyékok játékától a számítógépes algoritmusig
A Rupert-járat megtalálásának kulcsa egy geometriai trükk: képzeljük el, hogy a testet különböző irányokba forgatjuk, és közben megnézzük az árnyékait, ahogy felülről fény vetül rá. Ha például egy kocka egyik csúcsát felfelé fordítjuk, az árnyéka hatszög lesz. Az első, 17. századi felfedezés szerint a kocka „hatszög” árnyékába éppen belefér a „négyzet” árnyék, így ezen a tengelyen fúrható átjáró.
Bonyolultabb testeknél ezt a módszert számítógépek segítségével alkalmazzák, amelyek képesek végigpróbálni a lehetséges elfordulásokat, és keresik azt az esetet, amikor a második test árnyéka teljesen belefér az első, lyukasztott testen áthaladó nyílásba. Azonban néhány különösen szimmetrikus test, például a rumbikoszidodekaéder (rhombicosidodecahedron – 62 szabályos háromszögből, négyzetből és ötszögből álló alakzat) egyszerűen ellenáll minden ilyen algoritmusnak. De ez sem bizonyítja automatikusan, hogy nincs átjárat, hiszen a számítógép csak véges számú elfordulást tud vizsgálni, a lehetőségek száma pedig végtelen.
Bizonyítás: helyi és globális tételek kombinációja
Steininger és Yurkevich – akik a középiskolai matematikaversenyek óta barátok, és rendszeresen együtt ötletelnek – először közvetlenül generáltak lehetséges Nopert-jelölteket, majd speciális algoritmust dolgoztak ki. Fő ötletük az volt, hogy az orientációs paraméterteret (vagyis a két test viszonylagos elfordulásait) apró blokkokra osztották, és mindegyiket végigvizsgálták. Két fontos tételt használtak: az úgynevezett „globális tétel” nagyméretű tiltott blokkokat tud kizárni a lehetséges beállítások közül, míg a „helyi tétel” speciális, háromcsúcsú árnyékokat képes kizárni.
A Noperthedron esetén sikerült minden apró blokkra alkalmazni legalább az egyik tételt, így biztosan kizárták az összes lehetséges Rupert-járatot. Ez az első eset, hogy egy konvex poliéderről teljes bizonyossággal kimutatható: nem rendelkezik Rupert-tulajdonsággal. Állítólag egy fizikus rajongó már ki is nyomtatta 3D-ben ezt a furcsa, 150 háromszögből és két 15 oldalú sokszögből álló, vázára emlékeztető kristályt.
Mire jutunk ettől?
Lényeges, hogy egészen eddig általános elképzelés volt: minden sima, konvex test át tudja engedni önmagát önmagán – a Noperthedron viszont ennek frappáns ellenpéldája lett. A felfedezés nemcsak egy évszázados matematikai kérdést döntött meg, hanem új kutatási irányokat is nyitott: vajon milyen gyakoriak az ilyen, „önátmenet nélküli” testek? Tudunk-e egyszerűbb példákat találni, vagy csak extrém összetett formák esetén lehetetlen a Rupert-járat?
Mindezt figyelembe véve a Noperthedron megjelenése nemcsak egy régi fogadás igazságát ingatta meg, hanem új korszakot is nyitott a geometriában – kérdésekkel, amelyekre mostantól végre érdemes keresni a választ.