Az SAT egy standardizált teszt, amit az Egyesült Államokban a főiskolai felvételi eljárás során használnak. 1982-ben az SAT egyik kérdésén MINDEN diák elbukott. A kérdés így hangzott: Van két kör, A és B. Az A kör sugara harmada a B kör sugarának. Az A kör a B kör körül gurul. Hány fordulat után éri el az A kör középpontja ismét a kiindulási pontját? Lehetséges válaszok: A) 3/2, B) három, C) hat, D) 9/2, E) kilenc.
Az SAT kérdések gyors megoldásra lettek tervezve; ebben az esetben a diákoknak 25 feladatot kellett megoldaniuk 30 perc alatt. Sokan ösztönösen a B) három választ adták, mivel logikusnak tűnt, hogy ha a B kör kerülete háromszor akkora, mint az A köré, akkor az A körnek három teljes körbefordulásra van szüksége a B kör körül. Azonban mindenki tévedett, mivel a helyes válasz nem szerepelt a felsorolt lehetőségek között.
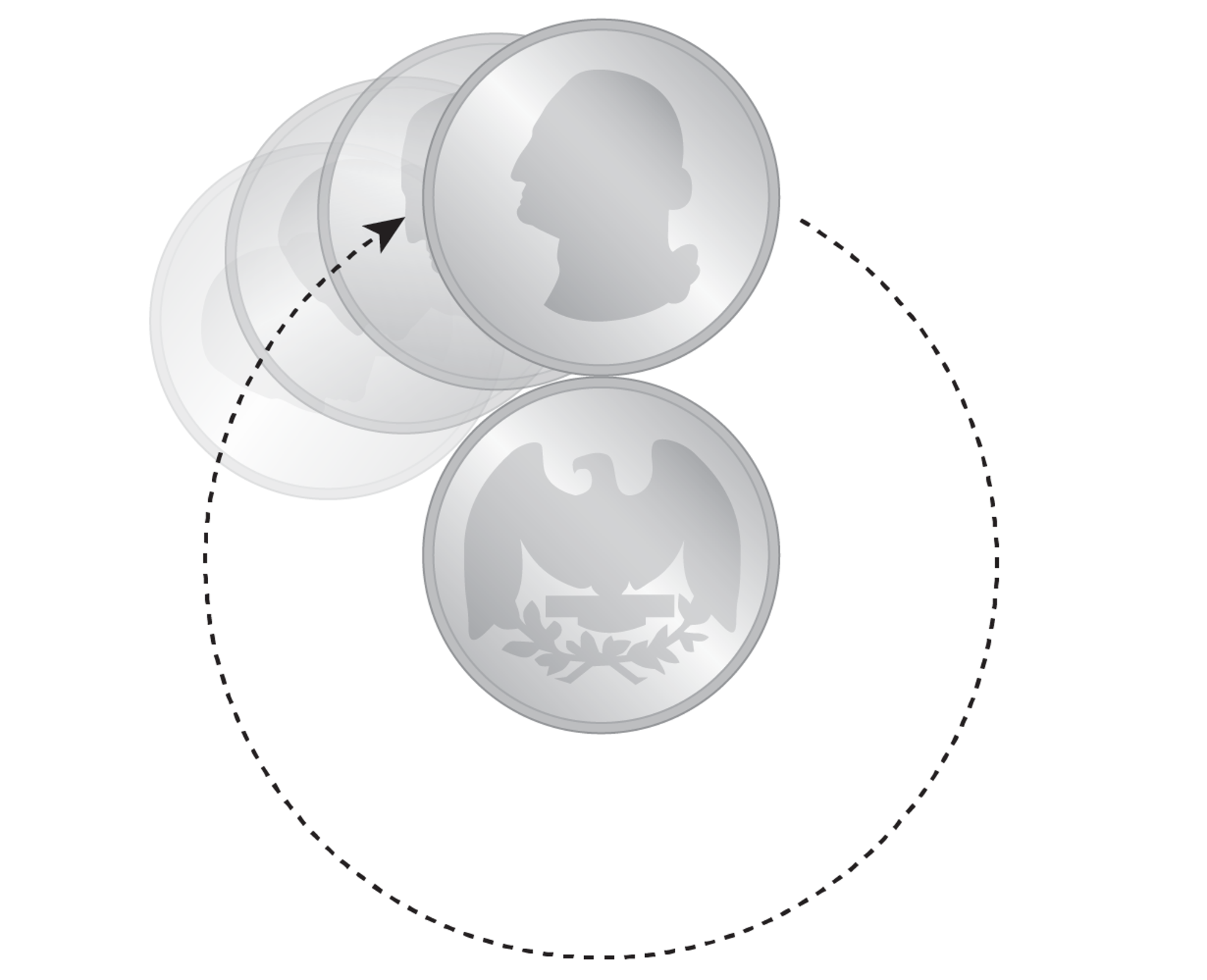
Amikor kiderült, hogy a teszt készítői is tévesen határozták meg a helyes választ, mindössze három diák — Shivan Kartha, Bruce Taub és Doug Jungreis — írt a College Boardnak, hogy felhívják a figyelmet a hibára. A probléma magyarázatához felhasználták a pénzérme forgás paradoxonát, amely azt mutatja, hogy ha két azonos érmét egymás körül forgatunk, az eredmény ellentmond az elsőre logikusnak tűnő következtetéseknek.
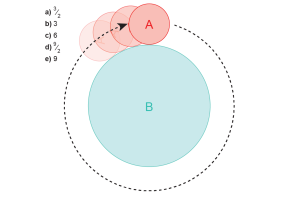
Az 1982-es SAT kérdés, amely körül az egész vitát folytatjuk, azt kérdezte, hogy hány fordulatot tesz az A kör, miközben a B kör körül gurul, amíg középpontja ismét vissza nem ér az eredeti kiindulási pontjához. Itt a kulcs a körök méreteinek arányában rejlik, amit sokan félreértelmeztek.
A helyes megoldás lépései:
- A körök aránya: Az A kör sugara harmada a B kör sugarának. Ez azt jelenti, hogy a B kör kerülete (2πR) háromszor nagyobb, mint az A kör kerülete (2πr).
- Alapvető logika: Ha csak simán az A kör kerületét vesszük alapul, akkor azt gondolhatnánk, hogy három fordulat szükséges az A körnek a B kör körül, mivel a B kör kerülete háromszorosa az A körének.
- Forgások számítása: Amikor az A kör gurul a B kör körül, nem csak egyszerűen “sétál” a kerületén, hanem forog is. A gurulás során az A kör minden egyes teljes fordulata megegyezik a saját kerületének hosszával.
- A pénzérme forgás paradoxon: Ezt a jelenséget használva megérthetjük, hogy miért forog többször az A kör. Amikor egy kör (vagy érme) gurul egy másik kör (vagy érme) körül, a forgási szám nem csak a két kör kerületének arányától függ. Mivel az A kör belső pontja (a középpont) visszatér az eredeti helyére, miközben az A kör a B kör külső kerületén gurul, az A körnek egy extra fordulatot kell tennie.
- A helyes válasz: Az A kör négy teljes fordulatot tesz a B kör körül, mivel a kiegészítő fordulatot is figyelembe kell venni, amit a mozgása miatt végez.
Ez a magyarázat alapul véve nem csak a körök egymáshoz viszonyított helyzetének fizikai tulajdonságait kell figyelembe venni, hanem a gurulás során keletkező extra mozgást is, ami a középpont ismételt eléréséhez szükséges. Ezért a helyes válasz négy fordulat, ami nem szerepelt a teszt válaszlehetőségei között, így minden diák téves választ adott.
A helyes válasz az volt, hogy az A kör négy fordulatot tesz a B kör körül, mivel a mozgása során egy extra fordulatot végez a fizikai elrendezés miatt. A diákok magyarázata alapján a College Board végül elismerte a hibát, és érvénytelenítette a kérdést a teszten.
Az eset rámutatott arra, hogy mennyire fontos a pontos fogalmazás és a problémák egyértelmű meghatározása a standardizált teszteken, amelyek jelentős hatást gyakorolhatnak a diákok továbbtanulási lehetőségeire. A hiba felismerése és a hozzáadott válasz fontos lecke volt a kritikus gondolkodás és a hibák elfogadásának fontosságában. Az esemény rávilágított arra is, hogy a standardizált tesztek szerepe változóban van, és a COVID-19 pandémia után sok egyetem már nem követeli meg ezeket a teszteket a felvételi eljárás során.
Ez a történet azt is bemutatja, hogyan segíthet a gyakorlatias problémamegoldás és a tudományos gondolkodás mélyebben megérteni a világ működését. A dokumentumban említett Brilliant.org oktatási platform például interaktív módon, játékos feladatok segítségével mélyítheti el a diákok tudását a természettudományok és matematika területén, ösztönözve őket, hogy aktívan részt vegyenek a tanulási folyamatban.
- SAT: Egy standardizált teszt, amit az Egyesült Államokban a főiskolai felvételi eljárás során használnak. A dokumentum egy hibás SAT kérdésre fókuszál.
- Kör A és Kör B: A problémás SAT kérdés két elemét jelölik. Kör A a kisebb, amelynek sugara egyharmada a Kör B sugarának, és Kör B körül gurul.
- College Board: Az a szervezet, amely az SAT vizsgát adminisztrálja. A dokumentumban említik, amikor a diákok jelentik a kérdésben talált hibát.
- Hiba: A dokumentum központi témája, amely arra utal, hogy a vizsga egyik kérdése helytelenül lett megfogalmazva, és emiatt minden diák rossz választ adott.
- Pénzérme forgás paradoxon (Coin Rotation Paradox): Egy fizikai jelenség, amely segít magyarázatot adni arra, hogy miért kell Kör A-nak több fordulatot tennie Kör B körül, mint amennyit elsőre várnánk.
- Oktatási Tesztelési Szolgáltatás (ETS): Az a szervezet, amely az SAT teszteket fejleszti és értékeli. A dokumentumban az ETS válasza a diákok által jelzett problémára kerül említésre.
- Kritikus gondolkodás: Az a képesség, amit a diákok megmutattak, amikor felismerték és jelentették a tesztkérdés hibáját. Fontos szerepet játszik a problémák megoldásában és az oktatásban.